Persamaan Garis Singgung Lingkaran Satu Titik Diluar Lingkaran, Persekutuan Dua Lingkaran Beserta Contoh Soal Dan Jawabannya
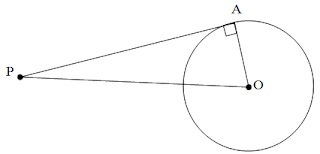
Dari gambar diatas dapat diketahui bahwa lingkaran bertitik pusat di O
dengan jari-jari OA dan OA tegak lurus dengan garis PA. Garis PA tersebut merupakan
garis singgung lingkaran melalui titip P di luar lingkaran. Dikarenakan setiap
sudut yang dibentuk oleh garis yang melalui titik pusat dan garis singgung
besarnya adalah 90 derajat, maka segitiga PAO merupakan segitiga siku-siku PAO.
Maka berlaku Theorema Phytagoras sebagai berikut (rumus).
rumus persamaan garis singgung satu titik
Contoh Soal:
Diketahui lingkaran berpusat di titik O dengan jari-jari OB = 3 cm.
Garis AB adalah garis singgung lingkaran yang melalui titik A di luar
lingkaran. Jika jarak OA = 5 cm maka tentukan panjang garis singgung AB.
Jawab:
Jadi panjang garis singgung AB pada gambar diatas adalah 4 cm.
2.
PERSAMAAN GARIS SINGGUNG PERSEKUTUAN DALAM DUA LINGKARAN
Persamaan Garis Singgung Persekutuan Dalam Dua Lingkaran
Garis Singgung Persekutuan Dalam Dua Lingkaran
Dari gambar gambar diatas dapat kita peroleh:
Jari-jari lingkaran yang berpusat di M = R;
Jari-jari lingkaran yang berpusat di N = r;
Panjang garis singgung persekutuan dalam = AB = d;
Jarak titik pusat kedua lingkaran = MN = p.
Jika garis AB digeser sejajar ke atas sejauh BN maka akan diperoleh
garis ON.
Garis ON sejajar garis AB, sehingga sudut MON = sudut MAB = 90 derajat
(sehadap).
Perhatikan segi empat ABQS.Garis AB//SQ, AS//BQ, dan sudut PSQ = sudut
PAB = 90o.
Jadi, segi empat ABNO merupakan persegi panjang dengan panjang AB = d
dan lebar BN = r.
Perhatikan bahwa segitiga MNO siku-siku di titik O. Dengan menggunakan
teorema Pythagoras diperoleh rumus panjang garis singgung persekutuan dalam dua
lingkaran sebagai berikut.
rumus panjang garis singgung persekutuan dalam dua lingkaran
Karena panjang ON = AB dan MO = R + r, maka rumus panjang garis singgung
persekutuan dalam dua lingkaran (d) dengan jarak kedua titik pusat p, jari-jari
lingkaran besar R, dan jari-jari lingkaran kecil r adalah.
rumus panjang garis singgung persekutuan dalam dua lingkaran
Contoh Soal:
Panjang jari-jari dua lingkaran masing-masing adalah 4 cm dan 3 cm.
Jarak kedua titik pusatnya adalah 25 cm. Hitunglah panjang garis singgung
persekutuan dalam kedua lingkaran tersebut!
Jawab:
jawaban panjang garis singgung persekutuan dalam dua lingkaran
Jadi, panjang garis singgung persekutuan dalam kedua lingkaran tersebut
adalah 24 cm.
3.
PERSAMAAN PANJANG GARIS SINGGUNG PERSEKUTUAN DUA LINGKARAN
Panjang Garis Singgung Persekutuan Dua Lingkaran
gambar garis singgung persekutuan dua lingkaran
Dari gambar persamaan panjang garis singgung persekutuan dua lingkaran
diatas dapat kita peroleh:
jari-jari lingkaran yang berpusat di M = R;
jari-jari lingkaran yang berpusat di N = r;
panjang garis singgung persekutuan luar adalah AB = l;
jarak titik pusat kedua lingkaran adalah MN = p.
Jika garis AB kita geser sejajar ke bawah sejauh BN maka diperoleh garis
ON.
Garis AB sejajar ON, sehingga sudut MON = sudut MAB = 90o (sehadap).
Perhatikan segi empat ABQS. Garis AB//SQ, AS//BQ, dan sudut PSQ = sudut
PAB = 90o.
Segitiga MNO siku-siku di O,
sehingga berlaku rumus sebagai berikut.
rumus panjang garis singgung
Karena panjang ON = AB dan MO = R – r, maka rumus panjang garis singgung
persekutuan luar dua lingkaran (l) dengan jarak kedua titik pusat p, jari-jari
lingkaran besar R, dan jari-jari lingkaran kecil r adalah sebagai berikut.
rumus panjang garis singgung persekutuan luar dua lingkaran
Contoh Soal:
Panjang jari-jari dua lingkaran masing-masing adalah 15 cm dan 5 cm.
Panjang garis singgung persekutuan luar kedua lingkaran adalah 24 cm. Hitunglah
jarak kedua titik pusat kedua lingkaran tersebut!
Jawab:
jawaban menentukan panjang garis singgung.png
Jadi jarak kedua titik pusat kedua lingkaran tersebut adalah 26 cm
0 Response to "Persamaan Garis Singgung Lingkaran Satu Titik Diluar Lingkaran, Persekutuan Dua Lingkaran Beserta Contoh Soal Dan Jawabannya"
Post a Comment