Persamaan Nilai Mutlak dan Cara Penyelesaiannya
Nilai mutlak sebuah bilangan merupakan jarak bilangan terhadap titik 0 pada garis bilangan tanpa memperhatikan arahnya. Pengertian tersebut kita ambil contoh |x| = 4 mempunyai dua buah penyelesaian dikarenakan ada dua buah bilangan yang jaraknya 4 titik dari 0 yaitu x = 4 dan x = -4. Hal ini bisa kalian lihat pada gambar berikut ini :
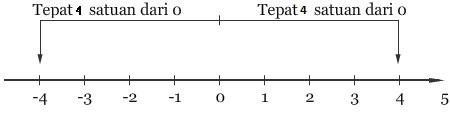
Konsep di atas bisa diperluas penggunaannya dalam menyelesaikan persoalan yang berkaitan dengan bentuk aljabar yang terletak pada simbol - simbol nilai mutlak. Hal ini dijelaskan oleh sifat persamaan nilai mutlak sebagai berikut :
"Apabila x merupakan sebuah bentuk aljabar, sedangkan n merupakan bilangan riil positif, maka |x| = n bisa diimplikasikan menjadi x = n atau x = -n"
Perlu diketahui bahwa sifat ini hanya bisa diaplikasikan sesudah kita melakukan isolasi terhadap simbol nilai mutlak yang ada pada satu ruas. Untuk lebih mudah memahaminya, perhatikan baik - baik pembahasan contoh soal persamaan nilai mutlak berikut ini :
Contoh Soal 1 :
Tentukanlah persamaan berikut ini :
-3 x -4 + 5 = 14
Penyelesaian :
Langkah pertama kita harus mengisolasi nilai mutlak caranya dengan memisahkan nilai mutlak agar berada pada satu ruas, sementara suku yang lain kita pindahkan menuju ruas yang lain. Sehingga :
-3 |x-4| + 5 = 14
-3 |x-4| = 14 - 5
-3 |x4| = 9
|x-4| = 3
Dalam persamaan nilai mutlak x - 4 adalah "X" sehingga bisa disimpulkan bahwa :
x - 4 = 3 atau x - 4 = -3
sehingga :
x = 7 atau x = 1
Jadi, himpunan penyelesaian dari persamaan tersebut adalah {7, 1}
Contoh Soal 2 :
Tentukan himpunan penyelesaian dari persamaan |4 - 2/5x| - 7 = 13
Penyelesaian :
|4 - 2/5x| - 7 = 13

"Apabila x merupakan sebuah bentuk aljabar, sedangkan n merupakan bilangan riil positif, maka |x| = n bisa diimplikasikan menjadi x = n atau x = -n"
Perlu diketahui bahwa sifat ini hanya bisa diaplikasikan sesudah kita melakukan isolasi terhadap simbol nilai mutlak yang ada pada satu ruas. Untuk lebih mudah memahaminya, perhatikan baik - baik pembahasan contoh soal persamaan nilai mutlak berikut ini :
Contoh Soal 1 :
Tentukanlah persamaan berikut ini :
-3 x -4 + 5 = 14
Penyelesaian :
Langkah pertama kita harus mengisolasi nilai mutlak caranya dengan memisahkan nilai mutlak agar berada pada satu ruas, sementara suku yang lain kita pindahkan menuju ruas yang lain. Sehingga :
-3 |x-4| + 5 = 14
-3 |x-4| = 14 - 5
-3 |x4| = 9
|x-4| = 3
Dalam persamaan nilai mutlak x - 4 adalah "X" sehingga bisa disimpulkan bahwa :
x - 4 = 3 atau x - 4 = -3
sehingga :
x = 7 atau x = 1
Jadi, himpunan penyelesaian dari persamaan tersebut adalah {7, 1}
Contoh Soal 2 :
Tentukan himpunan penyelesaian dari persamaan |4 - 2/5x| - 7 = 13
Penyelesaian :
|4 - 2/5x| - 7 = 13
|4 - 2/5x| = 13 + 7
|4 - 2/5x| = 20
maka :
|4 - 2/5x| = 20 atau |4 - 2/5x| = -20
|4 - 2/5x| = 20
maka :
|4 - 2/5x| = 20 atau |4 - 2/5x| = -20
sehingga :
-2/5x = 16
x = 16 x 5 : -2
= 80 : -40
atau
-2/5x = -24
x = -24 x 5 : -2
= -120 : -2
= 60
Jadi, himpunan penyelesaiannya adalah {-40, 60}
0 Response to "Persamaan Nilai Mutlak dan Cara Penyelesaiannya"
Post a Comment