Penjelasan Mengenai Jenis-Jenis Fungsi, Fungsi Baru dan Fungsi Lama, dan Model Matematika
Jenis-jenis fungsi diantaranya yaitu fungsi polinom, fungsi pangkat, fungsi akar, fungsi rasional,fungsi aljabar, fungsi trigonometri, fungsi eksponen, fungsi logaritma, fungsi transenden, fungsi sesepengga, fungsi genap dan fungsi ganjil, fungsi naik dan fungsi turun.
Fungsi Polinom
Fungsi polinom terdiri dari:
a. Fungsi Konstanta (Polinom Berderajat 0)
b. Fungsi Linear (Polinom Berderajat 1)
c. Fungsi Kuadratik (Fungsi Polinom Berderajat 2)
a. Fungsi Konstanta (Polinom Berderajat 0)
b. Fungsi Linear (Polinom Berderajat 1)
c. Fungsi Kuadratik (Fungsi Polinom Berderajat 2)
1. Aturan fungsi:
2. Daerah asal:

3. Daerah hasil bergantung pada bentuknya
Fungsi Konstanta (Polinom Berderajat 0)
1. Aturan fungsi: y = f(x) = a ; a merupakan konstanta
2. Daerah asal:
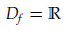
3. Daerah hasil:

4. Grafik:
Fungsi Linear (Polinom Berderajat 1)
1. Aturan fungsi: y = f(x) = ax + b ;
a dan b konstanta (a # 0)
a = kemiringan garis (gradien/slope)
b = perpotongan garis dengan sumbu-y (intersep)
2. Daerah asal:
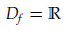
3. Daerah hasil:

4. Grafik:
Contoh 1:
Contoh 2:
Fungsi Kuadratik (Fungsi Polinom Berderajat 2)
1. Aturan fungsi: y = f(x) = ax^2 + bx + c
a, b, c merupakan kontanta dengan a # 0
Diskriminan: D = b^2 - 4ac
Titik maksimum/minimum: (x,y) = (-b/2a , -D/4a)
2. Grafik:
Fungsi Pangkat
1. Aturan fungsi : y = f(x) = x^n
2. Daerah asal:

3. Daerah hasil:
a. Jika n ganjil (misalnya, f(x) = x dan f(x) = x^3), maka

b. Jika n genap (misalnya, f(x) = x^2 dan f(x) = x^4), maka

4. Grafik
Fungsi Akar
1. Aturan fungsi:
2. Daerah asal:
Jika n ganjil :
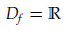
Jika n genap:

3. Daerah hasil:
Jika n ganjil:

Jika n genap:

4. Grafik:
Fungsi Rasional
1. Aturan Fungsi: y = f(x) = P(x)/Q(x)
2. Daerah asal:

3. Daerah hasil bergantung pada bentuknya
Fungsi Kebalikan
1. Aturan Fungsi: y = f(x) = 1/x ; x # 0
2. Daerah asal:
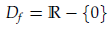
3. Daerah hasil:

4. Grafik:
Fungsi Aljabar
Definisi (Fungsi aljabar)
Fungsi f disebut fungsi aljabar jika fungsi tersebut dapat dibuat dengan menggunakan operasi aljabar, yaitu: penambahan, pengurangan, perkalian, pembagian, dan penarikan akar, yang dimulai dengan polinom.
Yang perlu di ingat: Funsi polinom, fungsi pangkat, fungsi akar, dan fungsi rasional merupakan fungsi aljabar.
Fungsi Trigonometri
Fungsi trigonometri terdiri dari fungsi sinus, fungsi kosinus, dan fungsi tangen.
Fungsi Sinus
1. Aturan fungsi: y = f(x) = sin x ; x dalam radian
2. Daerah asal:
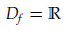
3. Daerah hasil:

4. Grafik:
Fungsi Kosinus
1. Aturan fungsi: y = f(x) = cos x ; x dalam radian
2. Daerah asal:
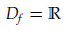
3. Daerah hasil:

4. Grafik
Fungsi Tangen
1. Aturan fungsi: y = f(x) = tan x = sin x/tan x
2. Daerah asal:

3. Daerah hasil:

4. Grafik:
Beberapa sifat fungsi trigonometri
- sin x = sin (x + 2pi)
- cos x = cos (x + 2pi)
- tan x = tan (x + pi )
- sin x [-1,1]
- cos x [-1,1]
Fungsi Eksponen
1. Aturan fungsi: y = f(x) = a^x ; a > 0
2. Daerah asal:
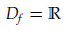
3. Daerah hasil:

4. Grafik:
Fungsi Logaritma
1. Aturan fungsi:
2. Daerah asal:

3. Daerah hasil:

4. Grafik:
Fungsi Transeden
Definisi (Fungsi transenden)
Fungsi transenden adalah fungsi yang bukan fungsi aljabar.
Himpunan fungsi transenden mencakup fungsi trigonometri, invers trigonometri, eksponen, dan logaritma.
Fungsi Sesepenggal
Definisi (Fungsi sesepenggal)
Fungsi sesepenggal adalah fungsi dengan banyak aturan dengan setiap aturan berlaku pada bagian tertentu dari daerah asal.
Fungsi Genap dan Fungsi Ganjil
Definisi (Fungsi genap)
Jika fungsi f memenuhi f(-x) = f(x) untuk setiap x di dalam daerah asalnya, maka fungsi f disebut fungsi genap.
Grafik fungsi genap simetri terhadap sumbu-y
Grafiknya:
Definisi (Fungsi ganjil)
Jika fungsi f memenuhi f(-x) = -f(x) untuk setiap x di dalam daerah asalnya, maka fungsi f disebut fungsi ganjil.
Grafik fungsi ganjil simetri terhadap titik asal
Grafiknya:
Fungsi Naik dan Fungsi Turun
Definisi (Fungsi naik)
Fungsi f disebut naik pada interval I jika f(x1) < f(x2) untuk setiap x1 < x2 di I
Definisi (Fungsi turun)
Fungsi f disebut naik pada interval I jika f(x1) > f(x2) untuk setiap x1 > x2 di I
Grafiknya:
Fungsi Baru dan Fungsi Lama
Dari fungsi dasar dapat dibentuk fungsi baru dengan cara:
- Transformasi fungsi: pergeseran, peregangan, dan pencerminan
- Operasi aljabar fungsi: penjumlahan, pengurangan, dan pembagian
- Komposisi fungsi
Misalkan c > 0. Untuk memperoleh grafik, maka:
- y = f(x) + c, geser grafik y = f(x) sejauh c satuan ke atas
- y = f(x) - c, geser grafik y = f(x) sejauh c satuan ke bawah
- y = f(x - c), geser grafik y = f(x) sejauh c satuan ke kanan
- y = f(x + c), geser grafik y = f(x) sejauh c satuan ke kiri
Seperti contoh grafik berikut:
Misalkan c > 1. Untuk memperoleh grafik, maka:
- y = c f(x), regangkan grafik y = f(x) secara tegak dengan faktor c
- y = 1/c f(x), mampatkan grafik y = f(x) secara tegak dengan faktor c
- y = f(cx), mampatkan grafik y = f(x) secara mendatar dengan faktor c
- y = f(1/c x), regangkan grafik y = f(x) secara mendatar dengan faktor c
Seperti contoh grafik berikut:
Transformasi Fungsi
Pencerminan (Refleksi)
Untuk memperoleh grafik, maka:
- y = - f(x), cerminkan grafik y = f(x) terhadap sumbu-x
- y = f(-x), cerminkan grafik y = f(x) terhadap sumbu-y
Seperti contoh grafik berikut:
Operasi Aljabar Fungsi
Definisi (Aljabar fungsi)
Komposisi Fungsi
Definisi (Komposisi fungsi)
Ilustrasi Komposisi Fungsi
Model Matematika
Definisi (Model matematika)
Model matematika adalah representasi dari fenomena dunia nyata yang melibatkan konsep atau formula matematik (sering kali menggunakan fungsi atau persamaan)
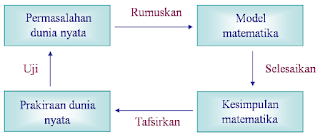
Proses permodelan:






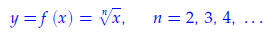

















0 Response to "Penjelasan Mengenai Jenis-Jenis Fungsi, Fungsi Baru dan Fungsi Lama, dan Model Matematika"
Post a Comment