Rangkuman Rumus Pada Integral Tigonometri - belajarmatematika.info Rangkuman Rumus Pada Integral Tigonometri - BELAJAR MATEMATIKA.info
› › › ›

Rangkuman Rumus Pada Integral Tigonometri

Friday, July 7, 2017 1 Comment Edit
Suatu fungsi trigonometri juga dapat diintegralkan. Untuk megintegralkan fungsi trigonometri ada beberapa rumus-rumus dasar yang perlu diketahui.
  1. Bentuk Baku Integral Trigonometri
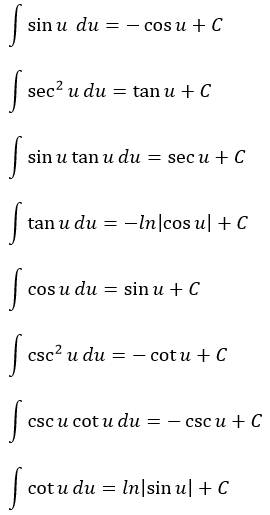
∫▒sin⁡〖u 〗 du=-cos⁡u+C ∫▒sec^2⁡u du=tan⁡u+C ∫▒〖sin⁡u tan⁡u 〗 du=sec⁡u+C ∫▒tan⁡u du=-ln|cos⁡u |+C ∫▒cos⁡u du=sin⁡u+C ∫▒csc^2⁡u du=-cot⁡u+C ∫▒〖csc⁡u cot⁡u 〗 du=-csc⁡u+C ∫▒cot⁡u du=ln|sin⁡u |+C
Selain rumus dasar integral di atas dalam mengintegralkan fungsi trigonometri juga digunakan identitas trigonometri. Berikut ini adalah beberapa identitas trigonometri yang sering digunakan.
  1. Identitas Trigonometri
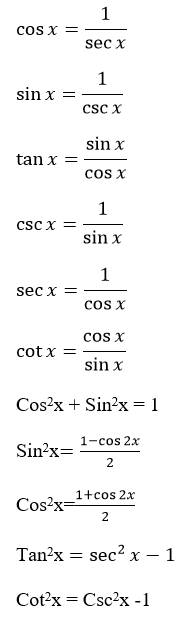
cos⁡〖x=1/sec⁡x 〗 sin⁡x=1/csc⁡x tan⁡x=sin⁡x/cos⁡x csc⁡x=1/sin⁡x sec⁡x=1/cos⁡x cot⁡x=cos⁡x/sin⁡x Cos2x + Sin2x = 1 Sin2x=(1-cos⁡2x)/2 Cos2x=(1+cos⁡2x)/2 Tan2x =sec^2⁡x-1 Cot2x = Csc2x -1
Subtitusi dalam integral trigonometri
Subtitusi juga digunakan dalam integral trigonometri yaitu dengan mengubah bentuk fungsi trigonometri menjadi bentuk baku yaitu dengan mengubah fungsi menggunakan identitas trigonometri.

Dalam mengerjakan soal integral trigonometri kita perlu melakukan permisalan dalam pemisalan tersebut biasanya yang dimisalkan diturunkan atau kita menggunakan diferensial. Sehingga kita juga perlu memahami konsep diferensial.
Diferensial suatu fungsi adalah sebagai berikut
Dx axn = n . axn-1
Contoh :
  1. ∫ Sin 5x dx tentukan integral tersebut !
Jawab :
Misal :
u = 5x
du = 5 dx
1/5 du = dx
sehingga
∫ Sin 5x dx = ∫ Sin u 1/5 du
Ganti 5x dengan permisalan sebelumnya yaitu u. kemudian subtitusikan dx yaitu 1/5 du.
= 1/5 ∫ Sin u du
Kemudian lihat bentuk baku integral dari sin yaitu –cos.
= – 1/5 cos u
Karena sudah diintegralkan maka lambang integralnya hilang dan di tambah + C di akhir jawaban. Kemudia jangan lupa untuk mensubtitusikan nilai u yaitu 5x
= – cos 5x + C
  1. Carilah
soal integral trigonometri
Jawab :
Perhatikan bentuk integral tersebut.
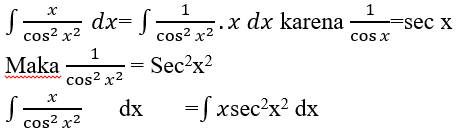
∫▒x/cos^2⁡〖x^2 〗 dx= ∫▒1/cos^2⁡〖x^2 〗 .x dx karena 1/cos⁡x =sec x Maka 1/cos^2⁡〖x^2 〗 = Sec2x2 ∫▒x/cos^2⁡〖x^2 〗 dx =∫▒xsec2x2 dx
Selanjutya kita melakukan pemisalan yaitu
U =x2
du =2x dx
1/2 du = x dx
Sehingga
∫▒1/2sec2u du = 1/2 ∫▒sec^2⁡u du = 1/2 tan u + C = 1/2 tan x2
  1. Carilah hasil dari integral trigonometri berikut ∫_0^(π/2)▒sin⁡6x dx
Jawab :
Misal :
U = 6x
du = 6dx
1/6 du = dx
Kemudian karen adalam soal terdapat batas yaitu (0, π/2). Sehingga kita harus mensubtitusikan batas tersebut ke pemisalan.
U = 6x
Untuk x=0
U = 6.0 = 0
Untuk x= π/2
U = 6. π/2= 3π
Maka batasnya sekarang berubah yaitu menjadi (0,3π)
Sehingga
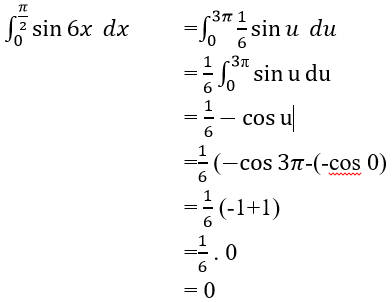
∫_0^(π/2)▒sin⁡6x dx =∫_0^3π▒〖1/6 sin〗⁡u du = 1/6 ∫_0^3π▒sin⁡u du = 1/6-cos⁡u =1/6 (〖-cos〗⁡3π-(-cos 0) = 1/6 (-1+1) =1/6 . 0 = 0
Ketika memiliki batas maka + C tidak perlu di tambakan saat hasil akhir.

Integral Parsial

Rumus integral parsial yaitu
rumus integral parsial
Contoh :
  1. ∫ (x + 3) cos (2x − π)dx =…..
    |____| |__________|
    u dv
Jawab :
Langkah pertama yaitu tentukan terlebih dulu mana u dan mana dv
Misalkan
(x + 3) adalah u, dan sisanya, cos (2x − π)dx sebagai dv,
u = (x + 3) …(Persamaan 1)
dv = cos (2x − π) dx …(Persamaan 2)
Langkah pertama selesai, kita tengok lagi rumus dasar integral parsial:
∫ u dv = uv − ∫v du
Terlihat di situ kita perlu u, perlu v dan perlu du. u nya sudah ada, tinggal mencari du dan v nya.
Dari persamaan 1, untuk menentukan du, caranya turunkan u nya,
u = (x + 3)
du/dx = 1
du = dx
Dari persamaan 2, untuk menentukan v,
dv = cos (2x − π)dx
atau
dv/dx = cos (2x − π)
dv/dx artinya turunan dari v adalah cos (2x − π), untuk mendapatkan v, berarti kita harus integralkan cos (2x − π) jika lupa, tengok lagi cara integral fungsi trigonometri,
v = ∫ cos (2x − π) dx = 1/2 sin (2x − π) + C
Kita rangkum lagi :
u = (x + 3)
v = 1/2 sin (2x − π)
du = dx
masukkan nilai-nilai yang sudah dicari tadi sesuai rumus integral parsial:
16 ∫ (x + 3) cos (2x − π)dx
Simpan dulu 16 nya, terakhir nanti hasilnya baru di kali 16
= uv − ∫v du
= (x + 3) 1/2 sin (2x − π) − ∫ 1/2 sin (2x − π) du
= 1/2 (x + 3) sin (2x − π) − ∫ 1/2 sin (2x − π) dx
= 1/2 (x + 3) sin (2x − π) − 1/2 {− 1/2 cos (2x − π) }
= 1/2 (x + 3) sin (2x − π) + 1/4 cos (2x − π)
kalikan 16, tambahkan + C nya
= 16 { 1/2 (x + 3) sin (2x − π) + 1/4 cos (2x − π) } + C
= 8 (x + 3) sin (2x − π) + 4 cos (2x − π) + C
  1. ∫ x sin 2x dx = …
Jawab :
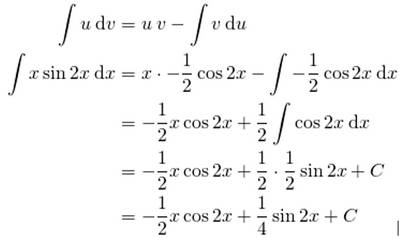
jawaban soal integral parsial nomor 2

1 Response to "Rangkuman Rumus Pada Integral Tigonometri"

  1. JennetJanuary 23, 2020 at 8:08 AM

    Concocted by Sir Isaac Newton, calculus figures numerical issues that are continually evolving. trig substitution

    ReplyDelete

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel