Penjelasan Lengkap Rumus ABC Untuk Menyelesaikan Persamaan Kuadrat

Pada kesempatan ini, saya akan berbagi sebuat tips atau cara-cara untuk menyelesaikan suatu persamaan kuadrat dengan menggunakan rumus yang secara umum kita sebut dengan Rumus ABC. Rumus ABC biasa digunakan apabila dalam penyelesaiannya cara pemfaktoran dan melengkapi kuadrat sempurna tidak dapat digunakan.

Sebelum melangkah ke cara menyelesaikan persamaan kuadrat dengan Rumus ABC. Saya akan review sedikit tentang menyelesaikan persamaan kuadrat dengan pemfaktoran dan melengkapi kuadrat sempurna.

Misalkan kita mempunyai suatu persamaan kuadrat seperti bentuk berikut ini:

AB = 0

Maka penyelesaian yang akan kita peroleh yaitu:

A = 0 atau B = 0

Dari permisalan diatas kita dapat mengetahui bahwa persamaan kuadrat $ax^{2}+bx+c=0$ dengan cara pemfaktoran yaitu dengan menentukan faktor dari perkalian ac (ac adalah konstanta) yang dimana b adalah penjumlahan dari a dan c.

Misalkan setelah difaktorkan kita ketahui hasilnya yaitu x dan y dimana x dan y adalah sebuah koefisien. maka perkalian luar dan perkalian dalam dari koefisien x dan y besarnya x dan y.

Contoh:

Tentukan himpunan penyelesaian dari $x^{2}-2x-8=0$ .

Jawab:

$x^{2}-2x-8=0$
(x - 4) (x + 2) = 0

x - 4 = 0 atau x + 2 = 0

x = 4 atau x = -2

Sehingga himpunan penyelesaian yang kita peroleh adalah x = 4 atau x = -2. Atau kita dapat tuliskan sebagai:

HP = {4 , -2}

Contoh:

Tentukan himpunan penyelesaian dari $6x^{2}-x-5=0$ .

Jawab:
$6x^{2}-x-5=0$
(6x + 5) (x - 1) = 0
6x + 5 = 0 atau x - 1 = 0

6x = -5 atau x = 1

x = -5/6

Sehingga himpunan penyelesaian yang kita peroleh adalah x = -5/6 atau x = 1. Atau kita dapat tuliskan sebagai:

HP = {-5/6 , 1}

Dua contoh di atas merupakan contoh untuk menentukan persamaan kuadrat dengan pemfaktoran. Selanjutnya akan diberikan penjelasan dan contoh singkat untuk menentukan persamaan kuadrat dengan melengkapi persamaan kuadrat.

Penyelesaian dengan cara melengkapi persamaan kuadrat ini lumayan rumit sehingga kita perlu sedikit teliti dalam menyelesaikan suatu persamaan.

Cara pengerjaan dengan metode ini yaitu:

Misalkan kita mempunyai persamaan berikut ini:

ax²– bx – c = 0

Maka yang harus kita lakukan adalah mengubah persamaan tersebut menjadi:

(x + p)² = q

Sehingga penyelesaian akhir yang akan kita peroleh yaitu x = -p + √q atau x = -p - √q. Atau kita dapat tuliskan dengan singkat menjadi:

x = -p ± √q

Berikut ini merupakan langkah-langkahnya:

Pertama-tama dari persamaan kuadrat yang diberikan, kita ubah persamaan tersebut menjadi bentuk seperti berikut ini:

$x^{2}+\frac{b}{a}x=-\frac{c}{a}$

Setelah kita ubah ke persamaan diatas, selanjutnya kita tambahkan kedua ruas tersebut dengan $\begin{pmatrix} \frac{b}{2a} \end{pmatrix}^{2}$ hal ini akan menjadikannya kuadrat sempurna.

Contoh:

Tentukan himpunan penyelesaian dari $x^{2}+13=6x$ .

Jawab:

$x^{2}+13=6x$

$x^{2}-6x+13=0$

$x^{2}-6x=-13$

$x^{2}-6x+\begin{bmatrix} \frac{1}{2}(6) \end{bmatrix}^{2}=-13+\begin{bmatrix} \frac{1}{2}(6) \end{bmatrix}^{2}$

$x^{2}-6x+9=-13+9$

$(x-3)^{2}=-4$

$x-3=\pm \sqrt{-4}$

$x_{1}= \sqrt{-4}+3$ atau $x_{2}= -\sqrt{-4}+3$

$x_{1}= 2i+3$ atau $x_{2}= -2i+3$

x=−2i+3

Sehingga himpunan penyelesaian yang kita peroleh adalah $x_{1}= 2i+3$ atau $x_{2}= -2i+3$ . Atau kita dapat tuliskan sebagai: HP = {2i + 3 , -2i + 3}

Nahhhhh, Sekarang kita akan masuk di penyelesaian persamaan kuadrat dengan Rumus ABC. Namun sebelumnya, seperti apa sihh Rumus ABC itu?

Rumus ABC sering dituliskan sebagai berikut:

$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

dengan $b^{2}-4ac$ merupakan Diskriminan dimana sering dituliskan dengan huruf D. Sehingga dapat dituliskan $D=b^{2}-4ac$ . Rumus inilah yang kita gunakan dalam menentukan akar-akar dari suatu persamaan kuadrat.

Contoh:

Tentukan akar-akar dari persamaan kuadrat $2x^{2}+3x-9=0$ .

Jawab:

Dari persamaan yang telah diberikan dan dengan mengacu pada Rumus ABC, kita dapat ketahui bahwa: a = 2 , b = 3 dan c = -9

Setelah kita mengetahui nilai a, b dan c, selanjutnya kita tinggal memasukan nilai a, b dan c tersebut ke dalam Rumus ABC. Sehingga akan seperti berikut ini:

$x_{1,2}=\frac{-3\pm\sqrt{3^2-4(2)(-9)}}{2(2)}$

Kemudian kita tinggal lanjut menghitungnya saja. Sehingga akan seperti berikut ini:

$=\frac{-3\pm\sqrt{3^2+72}}{4}$

$=\frac{-3\pm\sqrt{81}}{4}$

$=\frac{-3\pm9}{4}$

$x_{1}=\frac{-3+9}{4}$ atau $x_{2}=\frac{-3-9}{4}$

$x_{1}=\frac{6}{4}$ atau $x_{2}=-3$

Sehingga himpunan penyelesaian yang kita peroleh adalah x = 6/4 atau x = -3. Atau kita dapat tuliskan sebagai:

HP = {6/4 , -3}

Rumus ABC biasanya digunakan untuk menyelesaikan suatu persamaan kuadrat yang sulit difaktorkan. Bahkan ada orang lebih memilih menggunakan Rumus ABC sebagai cara utama, tanpa mencoba dengan pemfaktoran ataupun melengkapi bentuk kuadrat. Mengapa disebut Rumus ABC karena komponen-komponen yang ada dalam rumus hanya a, b dan c yang masing-masing merupakan koefisien dari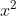 $x^{2}$ dan koefisien dari x.

Penjelasan Lengkap Rumus ABC Untuk Menyelesaikan Persamaan Kuadrat

0 Response to "Penjelasan Lengkap Rumus ABC Untuk Menyelesaikan Persamaan Kuadrat"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel