Cara Menghitung Jarak Titik ke Titik, Garis, dan Bidang
Cara Menghitung Jarak Titik ke Titik, Garis, dan Bidang - Dalam artikel kali ini akan dijelaskan beberapa kemungkinan yang terjadi untuk kedudukan titik terhadap titik, garis, ataupun bidang. Agar kalian bisa memahami materi ini, perhatikan baik - baik penjelasan di bawah ini.
Dalam gambar di atas terdapat dua buah titik, yaitu titik A dan titik B. Jarak kedua titik tersebut bisa ditentukan dengan cara menghubungkan titik A dan titik B dengan menggunakan sebuah garis. Panjang garis itulah yang menentukan jarak kedua titik tersebut. Sehingga, jarak dari titik A dengan titik B merupakan panjang ruas garis yang menghubungkan keduanya.
Perhatikan baik - baik contoh soal berikut ini :
Contoh Soal 1 :
Jika diketahui panjang rusuk pada kubus di atas adalah 6 cm dan titik X adalah pertengahan antara rusuk AB. Maka hitunglah jarak :
a. Titik H ke titik A
b. Titik H ke titik X
c. Titik H ke titik B
d. Titik E ke titik X
Penyelesaiannya :
a. Titik H ke titik A adalah panjang garis AH. Garis AH merupakan panjang diagonal sisi pada kubus tersebut, maka kita bisa menggunakan teorema phytagoras berikut ini :
A = √(EH2 + AE2)
= √(62 + 62)
= √(36 + 36)
= √72
= 6√2
b. Jarak titik H ke titik X adalah panjang garis HX. Panjang AX sama dengan setengah dari panjang rusuk AB, maka :
AX = 1/2 AB = 1/2 x 6 cm = 3 cm
dengan mengunakan teorema phytagoras :
HX = √(AH2 + AX2)
= √((6√2)2 + 32)
= √(72 + 9)
= √81
= 9 cm
c. Jarak titik H ke titik B adalah panjang garis BH. Garis BH merupakan panjang diagonal ruang pada kubus tersebut, oleh karenanya kita bisa menggunakan teorema phytagoras :
BH = √(AH + AB)
= √((6√2)2 + 62)
= √(72 + 36)
= √108
= 6√3 cm
d. Jarak titik E ke titik X adalah panjang garis EAX. Panjang AX sama dengan setengah dari panjang rusuk AB, maka :
AX = 1/2 AB = 1/2 x 6 cm = 3 cm
Dengan menggunakan teorema phytagoras :
EX = √(AE2 + AX2)
= √(62 + 32)
= √(36 + 9)
= √45
= 3√5 cm
Pada ambar di atas terdapat titik A dan garis g. Jarak antara titik A denan garis diperoleh dengan menarik garis dari titik A ke garis , garis tersebut berhenti di titik P sehingga terciptalah garis AP yang tegak lurus terhadap garis g. Jarak dari titik A ke garis g merupakan panjang dari garris AP. Sehingga, jarak antara titik dengan garis adalah panjang ruas garis yang ditarik dari titik tersebut secara tegak lurus terhadap garis tersebut.
Perhatikan contoh soal di bawah ini :
Contoh Soal 2 :
Perhatikan gambar berikut :
Sebuah kubus ABCD.EFGH memiliki panjang rusuk 6 cm dan titik X merupakan pertengahan diantara rusuk AB, maka hitunglah :
a. Jarak titik X ke garis DE
b. Jarak titik X ke garis CE
Penyelesaiannya :
Terlebih dahulu kita buatkan gambar seperti ini :
a. Jarak titik X ke garis DE adalah panjang garis dari titik X ke titik M yang posisinya tegak lurus terhadap garis DE, seperti pada gambar berikut ini :
DE = AH dan ME = 1/2 DE = 1/2 AH = 1/2 6√2 = 3√2
Dengan menggunakan teorema phytagoras :
MX = √(EX2 - ME2)
= √((3√5)2 - (3√2)2)
= √(45 - 18)
= √27
= 3√3
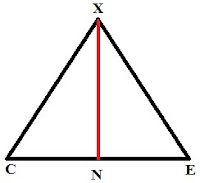
b. Jarak titik X ke garis CE adalah panjang garis dari titik X ke titik N yang posisinya tegak lurus terhadap garis CE, seperti pada gambar berikut ini :
CE = BH dan NE = 1/2 C = 1/2 BH = 1/2 6√3 = 3√3
Dengan menggunakan teorema phytagoras :
NX = √(EX2 - NE)2
= √((3√5)2 - (3√3)2)
= √(45 - 27)
= √18
= 3√2
Di dalam gambar di atas terdapat sebuah titik A dan bidang α. Jarak dari titik A ke bidang α bisa diketahui dengan cara menghubungkan titik A secara tegak lurus dengan bidang α. Sehingga, jarak dari suatu titik ke suatu bidang merupakan jarak dari titik tersebut ke proyeksinya pada bidang itu.
Perhatikan baik - baik contoh soal berikut ini :
Contoh Soal 3 :
Perhatikan gambar kubus ABCD.EFGH di bawah ini :
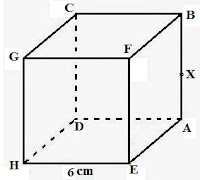
Jika diketahui panjang rusuk kubus di atas adalah 6 cm dan titik X adalah pertengahan antara rusuk AB. Maka hitunglah jarak dari titik X ke bidang CDEF!
Penyelesaiannya :
Buatlah gambar seperti di bawah ini :
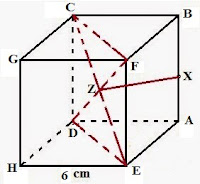
Jarak titik X ke bidang CDEF adalah panjang garis dari titik X ke titik Z yang tegak lurus terhadap bidang CDEF.
XZ = 1/2 AH = 1/2 6√2 = 3√2 cm.
Demikianlah pembahasan materi mengenai Cara Menghitung Jarak Titik ke Titik, Garis, dan Bidang. Semoga kalian bisa memahami penjelasan dan contoh soal yang diberikan dengan baik sehingga kalian tidak akan kesulitan lagi dalam menyelesaikan soal - soal yang berkaitan dengan materi ini. Selamat belajar!
Jarak Titik ke Titik Yang Lain
Coba kalian amati gambar berikut ini :Perhatikan baik - baik contoh soal berikut ini :
Contoh Soal 1 :
a. Titik H ke titik A
b. Titik H ke titik X
c. Titik H ke titik B
d. Titik E ke titik X
Penyelesaiannya :
a. Titik H ke titik A adalah panjang garis AH. Garis AH merupakan panjang diagonal sisi pada kubus tersebut, maka kita bisa menggunakan teorema phytagoras berikut ini :
A = √(EH2 + AE2)
= √(62 + 62)
= √(36 + 36)
= √72
= 6√2
b. Jarak titik H ke titik X adalah panjang garis HX. Panjang AX sama dengan setengah dari panjang rusuk AB, maka :
AX = 1/2 AB = 1/2 x 6 cm = 3 cm
dengan mengunakan teorema phytagoras :
HX = √(AH2 + AX2)
= √((6√2)2 + 32)
= √(72 + 9)
= √81
= 9 cm
c. Jarak titik H ke titik B adalah panjang garis BH. Garis BH merupakan panjang diagonal ruang pada kubus tersebut, oleh karenanya kita bisa menggunakan teorema phytagoras :
BH = √(AH + AB)
= √((6√2)2 + 62)
= √(72 + 36)
= √108
= 6√3 cm
d. Jarak titik E ke titik X adalah panjang garis EAX. Panjang AX sama dengan setengah dari panjang rusuk AB, maka :
AX = 1/2 AB = 1/2 x 6 cm = 3 cm
Dengan menggunakan teorema phytagoras :
EX = √(AE2 + AX2)
= √(62 + 32)
= √(36 + 9)
= √45
= 3√5 cm
Jarak Titik ke Garis
Perhatikan baik - baik gambar di bawah ini :Pada ambar di atas terdapat titik A dan garis g. Jarak antara titik A denan garis diperoleh dengan menarik garis dari titik A ke garis , garis tersebut berhenti di titik P sehingga terciptalah garis AP yang tegak lurus terhadap garis g. Jarak dari titik A ke garis g merupakan panjang dari garris AP. Sehingga, jarak antara titik dengan garis adalah panjang ruas garis yang ditarik dari titik tersebut secara tegak lurus terhadap garis tersebut.
Perhatikan contoh soal di bawah ini :
Contoh Soal 2 :
Perhatikan gambar berikut :
Sebuah kubus ABCD.EFGH memiliki panjang rusuk 6 cm dan titik X merupakan pertengahan diantara rusuk AB, maka hitunglah :
a. Jarak titik X ke garis DE
b. Jarak titik X ke garis CE
Penyelesaiannya :
Terlebih dahulu kita buatkan gambar seperti ini :
a. Jarak titik X ke garis DE adalah panjang garis dari titik X ke titik M yang posisinya tegak lurus terhadap garis DE, seperti pada gambar berikut ini :
DE = AH dan ME = 1/2 DE = 1/2 AH = 1/2 6√2 = 3√2
Dengan menggunakan teorema phytagoras :
MX = √(EX2 - ME2)
= √((3√5)2 - (3√2)2)
= √(45 - 18)
= √27
= 3√3
b. Jarak titik X ke garis CE adalah panjang garis dari titik X ke titik N yang posisinya tegak lurus terhadap garis CE, seperti pada gambar berikut ini :
CE = BH dan NE = 1/2 C = 1/2 BH = 1/2 6√3 = 3√3
Dengan menggunakan teorema phytagoras :
NX = √(EX2 - NE)2
= √((3√5)2 - (3√3)2)
= √(45 - 27)
= √18
= 3√2
Jarak Titik ke Bidang
Perhatikan baik - baik gambar di bawah ini :Perhatikan baik - baik contoh soal berikut ini :
Contoh Soal 3 :
Perhatikan gambar kubus ABCD.EFGH di bawah ini :
Jika diketahui panjang rusuk kubus di atas adalah 6 cm dan titik X adalah pertengahan antara rusuk AB. Maka hitunglah jarak dari titik X ke bidang CDEF!
Penyelesaiannya :
Buatlah gambar seperti di bawah ini :
Jarak titik X ke bidang CDEF adalah panjang garis dari titik X ke titik Z yang tegak lurus terhadap bidang CDEF.
XZ = 1/2 AH = 1/2 6√2 = 3√2 cm.
Demikianlah pembahasan materi mengenai Cara Menghitung Jarak Titik ke Titik, Garis, dan Bidang. Semoga kalian bisa memahami penjelasan dan contoh soal yang diberikan dengan baik sehingga kalian tidak akan kesulitan lagi dalam menyelesaikan soal - soal yang berkaitan dengan materi ini. Selamat belajar!
0 Response to "Cara Menghitung Jarak Titik ke Titik, Garis, dan Bidang"
Post a Comment