Pembahasan Lengkap Materi Integral Matematika

Yang akan kita bahas kali ini menganai - Anti Turunan, Luas di Bawah Kurva, Integral Tentu, Integral Tak Tentu, Teorema Dasar Kalkulus Dan Aturan Substitusi
Beberapa terapan integral dalam kehidupan sehari-hari:

Peramalan jumlah populasi pada masa untuk beberapa tahun yang akan datang.
Penentuan konsumsi energi di Bandung pada suatu hari.
Penentuan ketinggian pesawat ulang-alik pada waktu tertentu.

Anti Turunan

Definisi dari anti turunan

Fungsi F disebut anti turunan dari fungsi f pada interval I jika F'(x) = f(x) untuk setiap $x\in I$ .

Teorema anti turunan secara umum
Jika F anti turunan dari f pada interval I, maka anti turunan dari f yang paling umum adalah F(x) + C dengan C adalah konstanta sembarang.

Formula-formula anti turunan

1. Fungsi: kf(x) ; Anti turunan: kF(x) + C ; k=konstanta, C=konstanta

2. Fungsi: f(x) $\pm$ g(x) ; Anti turunan: F(x) $\pm$ G(x) + C

3. Fungsi: $x^{n}, n\neq -1$ ; Anti turunan: $x^{n+1}/{(n+1)}+C$ ; C=konstanta

4. Fungsi: sin x ; Anti turunan: -cos x + C; C=konstanta

5. Fungsi: cos x ; Anti turunan: sin x + C; C=konstanta

6. Fungsi: $sec^{2}(x)$ ; Anti turunan: tan x + C; C=konstanta

7. Fungsi: $csc^{2}(x)$ ; Anti turunan: -cot x + C; C=konstanta

8. Fungsi: sec x tan x ; Anti turunan: sec x + C; C=konstanta

9. Fungsi: csc x cot x ; Anti turunan: -csc x + C; C=konstanta

Luas di Bawah Kurva

Konsep integral dapat didekati dengan gagasan penentuan luas daerah bidang rata
Bagaimana menentukan luas daerah bidang rata s yang dibatasi oleh kurva $y=f(x)\geq 0$ , sumbu-x, garis x = a, x = b? Lihat grafik di atas

Pendekatan persegi panjang untuk menghitung luas

Buat n persegi panjang dengan luas $A_{1},A_{2},A_{3},...,A_{n}$
Luas A dari daerah S didekati dengan penjumlahan luas n persegi panjang
Makin besar n, luas n persegi panjang makin mendekati luas A
Luas A didefinisikan sebagai penjumlahan takhingga banyak persegi panjang

Lihat gambar di bawah ini:

Perhitungan luas dengan pendekatan persegi panjang

Untuk menentukan luas daerah S yang dibatasi oleh kurva kontinu 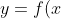$y=f(x)\geq 0$ sumbu-x, garis x = a, x = b, maka lakukan:

Bagi interval [a,b] menjadi n interval bagian $[a=x_{0},x_{1}],[x_{1},x_{2}],...,[x_{n-1},x_{n}]$ dengan sama panjang, yakni $\Delta x=\frac{b-a}{n}$ , sehingga akan berlaku $x_{i}=a+i\Delta x$
Pada setiap interval bagian $[x_{i-1},x_{i}]$ buat persegi panjang dengan lebar $\Delta x$ dan panjang $f(x_{i})$ , sehingga luas $A_{i}=f(x_{i})\Delta x$

dengan i = 1,2,3,...

Definisi luas di bawah kurva
Luas A dari daerah S yang dibatasi oleh kurva kontinu $y=f(x)\geq 0$ sumbu-x, garis x = a, x = b adalah:
$A=\lim_{n\rightarrow \infty }R_{n}=\lim_{n\rightarrow \infty }\sum_{i=1}^{n}f(x_{i})\Delta x=\lim_{n\rightarrow \infty }[f(x_{1})\Delta x+f(x_{2})\Delta x+...+f(x_{n})\Delta x]$

$R_{n}$ adalah Jumlah Riemen

Berikut ini diberikan formula notasi sigma, diantaranya:

$1. \sum_{i=1}^{n}c=cn ;$

$2. \sum_{i=1}^{n}cx_{i}= c\sum_{i=1}^{n}x_{i}$

$3. \sum_{i=1}^{n}x_{i}\pm y_{i} = \sum_{i=1}^{n}x_{i}\pm \sum_{i=1}^{n}y_{i}$

$4. \sum_{i=1}^{n}i = \frac{n(n+1)}{2}$

$5. \sum_{i=1}^{n}i^{2} = \frac{n(n+1)(2n+1)}{6}$

$6. \sum_{i=1}^{n}i^{3} = \left ( \frac{n(n+1)}{6} \right )^{2}$

dengan c adalah konstanta

Integral Tentu

Konsep jumlah Rieman 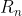$R_{n}$ (pada luas di bawah kurva) dapat diperluas untuk daerah yang ada di bawah sumbuh-x atau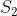 $S_{2}$

Jumlah Riemen pada 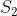$S_{2}$ negatif karena $f(x_{i})< 0$

Pada interval [a,b], lambang pada limit jumlah Rieman dapat diganti dengan lambang integral tentu

$\lim_{n\rightarrow \infty }\sum_{i=1}^{n}f(x_{i})\Delta x=\int_{a}^{b}f(x)dx$

Perhatikan grafik di bawah ini:

Definisi integral tentu
Integral tentu fungsi f dari a ke b adalah
$\int_{a}^{b}f(x)dx=\lim_{n\rightarrow \infty }\sum_{i=1}^{n}f(c_{i})\Delta x$
dengan:
$c_{i}\in \left [ x_{i-1},x_{i} \right ]$ ; $\Delta x=\frac{b-a}{n}$ ; $[ x_{i-1},x_{i} ]$ adalah interval bagian ke-i dari $[a,b]=[x_{0},x_{n}]$ dimana i adalah 1,2,....

Hasil Evaluasi Integral Tentu

$\int_{a}^{b}f(x)dx, b\geq a$

menghasilkan sebuah bilangan dengan salah satu dari tiga kemungkinan berikut:

1. Apabila lebih besar 0 ( >0 )

- Seluruh daerah berada di atas sumbu-x

- Luas daerah di atas sumbu-x > luas daerah di bawah sumbu-x

2. Apabila lebih kecil 0 ( < 0 )

- Seluruh daerah berada di bawah sumbu-x

- Luas daerah di bawah sumbu-x > luas daerah di atas sumbu-x

3. Apabila sama dengan 0 ( = 0 )

- f (x) = 0 atau a = b

- Luas daerah di bawah sumbu-x = luas daerah di atas sumbu-x

Sifat-Sifat Integral Tentu

Berikut adalah sifat-sifat umum dari integral tentu:

$1. \int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx$

$2. \int_{a}^{a}f(x)dx=0$

$3. \int_{a}^{b}cdx=c(b-a)$

$4. \int_{a}^{b}cf(x)dx=c \int_{a}^{b}f(x)dx$

$5. \int_{a}^{b}[f(x)\pm g(x)]dx= \int_{a}^{b}f(x)dx\pm \int_{a}^{b}g(x)dx$

$6. \int_{a}^{b}f(x)dx +\int_{b}^{c}f(x)dx= \int_{a}^{c}f(x)dx$

Teorema Dasar Kalkulus (TDK)

Kalkulus diferensial muncul dari permasalahan garis singgung.
Kalkulus integral muncul dari permasalahan luas daerah: perhitungan rumit seperti limit Jumlah Riemann.
Konsep yang mengaitkan kalkulus integral dengan kalkulus diferensial: Teorema Dasar Kalkulus (TDK).
Dengan TDK, perhitungan integral dan aplikasinya menjadi jauh lebih
mudah karena merupakan kebalikan dari proses turunan.

Ilustrasi geometri teorema dasar kalkulus 1

Teorema dari Teorema dasar kalkulus 1
Jika f kontinu di [a,b] maka $F(x)= \int_{a}^{x}f(t)dt$ kontinu pada [a,b], terturunkan pada (a,b), dan turunnannya adalah f(x)
$F'(x)= \frac{\mathrm{d} }{\mathrm{d} x}\int_{a}^{x}f(t)dt=f(x)$

Teorema Dasar Kalkulus 2

Teorema dari teorema dasar kalkulus 2
Jika f kontinu pada [a,b] dan F sebarang anti turunan f pada [a,b], maka:
$\int_{a}^{b}f(x)dx=F(b)-F(a)$

Teorema dasar kalkulus 2 memberi cara yang mudah dalam mengevaluasi integral tentu,

jauh lebih mudah dibandingkan menggunakan limit Jumlah Riemann.

Berdasarkan teorema dasar kalkulus 2, untuk mengevaluasi integral tentu f pada [a, b]:

1. Tentukan anti turunan F dari f ,

2. Evaluasi F(b) - F(a) .

Integral Tak Tentu

Definisi integral tak tentu
Misalkan F adalah anti turunan f Integral taktentu f(x) terhadap x adalah
$\int f(x)dx=F(x)+C$

- Hasil integral tentu berupa suatu bilangan sedangkan hasil integral taktentu berupa fungsi.

- Integral taktentu adalah lambang lain anti turunan.

Formula Integral Tak Tentu

Berikut ini disajikan beberapa formula dari integral tak tentu, diantaranya:

$1. \int kf(x)dx=k\int f(x)dx$

$2. \int [f(x)\pm g(x)]dx=\int f(x)dx\pm \int g(x)dx$

$3. \int x^{n}dx=x^{n+1}/(n+1)+C , n\neq -1$

$4. \int sinxdx= -cos x +C$

$5. \int cosxdx= sin x +C$

Aturan Substitusi

Aturan substitusi digunakan pada kasus:

- Sulit menentukan anti-turunan integran secara langsung, tetapi

- Bagian tertentu integran dapat dimisalkan dengan variabel baru sehingga lebih mudah dicari anti-turunannya.

Teorema aturan substitusi
Jika u = g(x) adalah fungsi terturunkan dan f kontinu pada $W_{g}$ , maka
$\int f(g(x))g'(x)dx=\int f(u)du$
$\int_{a}^{b}f(g(x))g'(x)=\int_{g(a)}^{g(b)}f(u)du$