Rangkuman Materi Limit dan Kekontinuan Dalam Kalkulus
Limit Fungsi
Limit Fungsi di Suatu Titik
Menggambarkan perilaku fungsi jika peubahnya mendekati suatu titik.
Dari tabel dan grafik: nilai f (x) dapat dibuat sedekat mungkin ke 3, dengan cara mengambil x yang cukup dekat ke 1, tetapi x # 1
Notasi:=3)
Definisi (Limit fungsi di suatu titik)
Misalkan fungsi f terdefinisi pada interval terbuka I yang memuat a, kecuali mungkin di a. Limit f (x) ketika x mendekati a sama dengan L, ditulis
Apabila nilai f (x) dapat dibuat sedekat mungkin ke L, dengan cara mengambil nilai x yang cukup dekat ke a, tetapi x # a.
Kasus-kasus Limit yang Sama
Ketiga kasus di bawah ini memberikan limit yang sama, yaitu=L)
Ketiga kasus di bawah ini memberikan limit yang sama, yaitu
Limit Satu Sisi
Menggambarkan perilaku fungsi jika peubahnya mendekati suatu titik dari satu arah saja, kiri atau kanan
Ilustrasi:
Diketahui: f (x) = [[x]], x anggota dari 2 [-1, 2)
Dari grafik:
1) nilai f (x) dapat dibuat sedekat mungkin ke -1, dengan cara mengambil x yang cukup dekat ke 0 dari arah kiri dan x # 0.
Notasi: =-1)
2) nilai f (x) dapat dibuat sedekat mungkin ke 0, dengan cara mengambil x yang cukup dekat ke 0 dari arah kanan dan x # 0.
Notasi: =-1)
Definisi (limit kanan)
Misalkan fungsi f terdefinisi pada interval [a, b), kecuali mungkin di a. Limit kanan f (x) ketika x mendekati a (limit f (x) ketika x mendekati a dari sisi kanan) sama dengan L, ditulis
apabila nilai f (x) dapat dibuat sedekat mungkin ke L, dengan cara mengambil nilai x yang cukup dekat ke a dan x > a.
Definisi (limit kiri)
Misalkan fungsi f terdefinisi pada interval (b, a], kecuali mungkin di a. Limit kiri f (x) ketika x mendekati a (limit f (x) ketika x mendekati a dari sisi kiri) sama dengan L, ditulis
apabila nilai f (x) dapat dibuat sedekat mungkin ke L, dengan cara mengambil nilai x yang cukup dekat ke a dan x < a.
Teorema (hubungan limit di suatu titik dengan limit satu sisi)
Limit Tak Hingga
Menggambarkan perilaku nilai fungsi yang membesar atau mengecil tanpa batas jika peubahnya mendekati suatu titik
Ilustrasi:
Diketahui: 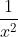
Dari grafik:
nilai f (x) dapat dibuat sebesar mungkin, dengan cara mengambil x yang cukup dekat ke 0, tetapi x # 0.
Notasi: =%5Cinfty)
Definisi
Misalkan fungsi f terdefinisi pada interval terbuka I yang memuat a, kecuali mungkin di a. Limit f (x) ketika x mendekati a sama dengan, ditulis
apabila nilai f (x) dapat dibuat sebesar mungkin, dengan cara mengambil nilai x yang cukup dekat ke a, tetapi x # a.
Catatan:
Notasi lain untuk limit f (x) ketika x mendekati a sama dengan 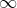 adalah f(x) -->
adalah f(x) --> 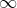 bila x--> a
bila x--> a
Ilustrasi:
Diketahui: f(x) = - 1/x^2
Dari grafik:
nilai f (x) dapat dibuat sekecil mungkin, dengan cara mengambil x yang cukup dekat ke 0, tetapi x # 0.
Notasi: &space;-&space;%5Cinfty)
Definisi
Misalkan fungsi f terdefinisi pada interval terbuka I yang memuat a, kecuali mungkin di a. Limit f (x) ketika x mendekati a sama dengan, ditulis
apabila nilai f (x) dapat dibuat sekecil mungkin, dengan cara mengambil nilai x yang cukup dekat ke a tetapi x # a.
Catatan:
Notasi lain untuk limit f (x) ketika x mendekati a sama dengan  adalah f(x) -->
adalah f(x) -->  bila x--> a
bila x--> a
Definisi serupa dapat diberikan untuk limit tak-hingga satu sisi:
Hukum Limit
Teorema Limit Utama
Teorema
Misalkan c konstanta, n bilangan bulat positif dan kedua limit ) dan
dan )
ada, maka :
Teorema:
Teorema Substitusi
Teorema
Jika f adalah polinom atau fungsi rasional dan a di dalam daerah asal f, maka =f(a))
Pertidaksamaan Limit
Teorema
Jika f (x) ≤ g (x) pada waktu x dekat a (kecuali mungkin di a) dan limit f dan g keduanya ada untuk x mendekati a, maka
Teorema Apit
Teorema
Teorema
Jika f (x) ≤ g (x) ≤ h (x) pada waktu x dekat a(kecuali mungkin di a)
dan =L%3D&space;%5Clim_%7Bx&space;%5Cto&space;a&space;%7Dh(x),) , maka
, maka =L)
Kekontinuan Fungsi
Kekontinuan di Satu Titik
Definisi (Kekontinuan di satu titik)
Misalkan fungsi f terdefinisi pada interval I yang memuat a. Fungsi f disebut kontinu di a, bila&space;f(a))
Catatan:
Operasi Aljabar Fungsi Kontinu di Satu Titik
Teorema:
Jika fungsi f dan g kontinu di x = a dan c adalah konstanta, maka fungsi-fungsi berikut juga kontinu pada a:
1) f + g
2) f - g
3) cf
4) fg
5) f/g jika g(a) # 0
Limit dan Kekontinuan Fungsi Komposit
Teorema (Limit fungsi komposit)
Jika f kontinu pada b dan &space;b) , maka
, maka )&space;f(%5Clim_%7Bx&space;%5Cto&space;a&space;%7Dg(x)))
Teorema (Kekontinuan fungsi komposit)
Jika fungsi g kontinu pada a dan f kontinu pada g (a), maka fungsi komposit f o g kontinu pada a.
Kontinu Kiri dan Kontinu Kanan
Definisi (Kontinu kiri)
Misalkan fungsi f terdefinisi pada interval (b, a]. Fungsi f disebut kontinu kiri di a, bila
&space;f(a))
Definisi (Kontinu kanan)
Misalkan fungsi f terdefinisi pada interval (b, a]. Fungsi f disebut kontinu kiri di a, bila&space;f(a))
Kekontinuan pada Interval
Definisi (Kekontinuan pada interval)
- Fungsi f kontinu pada interval (a, b), jika f kontinu di setiap titik pada interval tersebut.
- ungsi f kontinu pada interval [a, b], jika f kontinu pada interval (a, b), kontinu kanan di a dan kontinu kiri di b
Fungsi-fungsi berikut kontinu pada daerah asalnya:
- Fungsi polinom
- Fungsi rasional
- Fngsi trigonometri
- Fungsi akar
- Fungsi eksponen
- Fungsi logaritma
- Fungsi nilai mutlak
Teorema Nilai Antara
Teorema
Jika fungsi f kontinu pada interval tertutup [a, b] dan N adalah bilangan di antara f (a) dan f (b), maka terdapat c anggota dari (a, b) sedemikian sehingga f (c) = N.
Kegunaan Teorema Nilai Antara
1) Menunjukkan keberadaan akar suatu persamaan pada suatu interval.
2) Menunjukkan keberadaan penyelesaian suatu persamaan pada suatu interval.
3) Menunjukkan keberadaan titik potong dua kurva pada suatu interval.





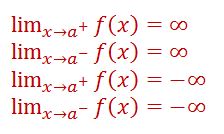




0 Response to "Rangkuman Materi Limit dan Kekontinuan Dalam Kalkulus"
Post a Comment