Materi Aturan Turunan Matematika

Aturan Rantai

Misalkan ingin ditentukan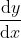 $\frac{\mathrm{d} y}{\mathrm{d} x}$ bagi $y=(x^{2}-3x)^{2}$ .
Teknik penyelesaian
1. Kuadratkan, karena bentuknya masih sederhana:
$(x^{2}-3x)(x^{2}-3x)= x^{4}-6x^{3}+9x^{2}$
sehingga, $y= x^{4}-6x^{3}+9x^{2}$
$y= 4x^{3}-18x^{2}+18x$

2. Pemisahan variabel baru:
misalkan: $y= u^{2}, u=x^{2}-3x$

sehingga,
$\frac{\mathrm{d} y}{\mathrm{d} u}=2u , \frac{\mathrm{d} u}{\mathrm{d} x}=2x-3$
maka,
$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\mathrm{d} y}{\mathrm{d} u}\frac{\mathrm{d} u}{\mathrm{d} x} =2u(2x-3)=2(x^{2}-3x)(2x-3)=(2x^{2}-6x)(2x-3)$
dengan demikian akan diperoleh:
$\frac{\mathrm{d} y}{\mathrm{d} x}=4x^{3}-18x^{2}+18x$
hasil akhir yang diperoleh sama dengan cara 1

Catatan:
Apabila persamaannya sederhana, kita dapat menggunakan teknik 1. Namun apabila persamaannya seperti $(x^{2}+3x)^{2016}$ maka akan rumit dalam mencari $\frac{\mathrm{d} y}{\mathrm{d} x}$ namun akan efisien jika menggunakan ke 2. Teknik ke 2 disebut juga dengan aturan rantai.

Teorema (Aturan rantai)

Misalkan f(u) terturunkan di u=g(x) dan g(x) terturunkan di x, maka fungsi komposit (f o g) (x) terturunkan di x dan (f o g)' (x) = f ' (g(x))g'(x)
Dengan notasi Leibniz, jika y = f(u) dan u = g(x), maka $\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\mathrm{d} y}{\mathrm{d} u}\frac{\mathrm{d} u}{\mathrm{d} x}$

Berikut diberikan Ilustrasi Aturan Rantai (komposisi dua fungsi)

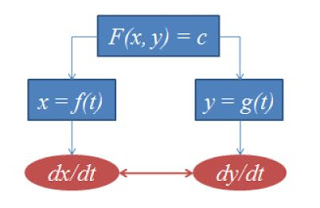
Berikut diberikan Ilustrasi Aturan Rantai (komposisinya lebih dari dua fungsi)

Turunan Implisit

Fungsi Eksplisit : y=f(x))

contohnya, $y= 2x-1 , y=\sqrt{1-x^{2}}$

Fungsi Implisit: F(x,y)=c

. Dengan c (konstanta) dan dengan asumsi y fungsi terhadap x
Contohnya:
y-2x-1=0

$x^{2}+y^{2}=1$
$sin(xy)+2x^{2}=3$

Langkah-langkah menurunkan fungsi implisit:
1. Turunkan kedua ruasnya terhadap x
2. Gunakan aturan rantai
3. Kemudian tentukan $\frac{\mathrm{d} y}{\mathrm{d} x}$

Turunan Fungsi Pangkat Rasional

Teorema

Misalkan p, q adalah bilangan bulat,
$\frac{\mathrm{d} }{\mathrm{d} x}x^{p/q}=\frac{p}{q}x^{p/q-1}, q\neq 0$

Turunan Tingkat Tinggi

$\frac{\mathrm{d} ^{n}y}{\mathrm{d} x^{n}}=\frac{\mathrm{d} }{\mathrm{d} x}\left ( \frac{\mathrm{d} ^{n-1}y}{\mathrm{d} x^{n-1}} \right )$

Aplikasi Turunan Kedua dalam Penentuan Percepatan

Jika s = f(t) menyatakan fungsi posisi objek pada waktu t yang bergerak pada garis lurus, maka:

$v(t)=\frac{\mathrm{d} s}{\mathrm{d} t}=f'(t)$ menyatakan kecepatan objek pada waktu t
$a(t)=\frac{\mathrm{d} v}{\mathrm{d} t}=\frac{\mathrm{d} ^{2}s}{\mathrm{d} t^{2}}=f''(t)$ menyatakan percepatan objek pada waktu t

Laju Terkait

Bila terdapat suatu kaitan antar variabel serta masing-masing variabel bergantung pada waktu t, maka perubahan laju dalam satu variabel dapat berakibat perubahan laju pada variabel lainnya.

Makna dari tanda laju:

Misalkan:
$\frac{\mathrm{d} x}{\mathrm{d} t}> 0$
apabila t membesar maka x membesar
apabila t mengecil maka x mengecil

$\frac{\mathrm{d} x}{\mathrm{d} t}< 0$
apabila t membesar maka x mengecil
apabila t mengecil maka x membesar

$\frac{\mathrm{d} x}{\mathrm{d} t}=0$
maka x-nya konstan

Strategi Menyelesaikan Masalah Laju Terkait

Pahami permasalahan.
Buat diagram, berikan notasi kepada variabel-variabel yang merupakan fungsi terhadap waktu
Nyatakan informasi dan laju yang diketahui dalam bentuk turunan.
Tuliskan persamaan yang mengaitkan variabel yang diketahui.
Gunakan aturan rantai untuk menurunkan kedua ruas terhadap t.
Substitusi informasi yang diketahui dan tentukan laju yang diinginkan.

Materi Aturan Turunan Matematika

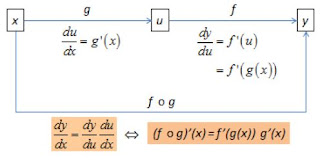
0 Response to "Materi Aturan Turunan Matematika"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel