Penjumlahan dan Pengurangan Dan Perkalian Matriks Dengan Skalar
Matriks merupakan kumpulan bilangan yang disusun dalam bentuk persegi panjang atau bujur sangkar. Pemberian nama pada matriks ditulis dengan huruf besar, misalnya A, B, C,...,Z, dan setiap matriks akan mempunyai baris dan kolom.
Banyaknya baris dan kolom ini menentukan ukuran atau ordo matriks. Misalnya matriks A mempunyai baris sebanyak m dan kolom sebanyak n, maka ordo matriks A adalah m x n, dengan m dan n merupakan bilangan bulat positif. Secara umum dapat ditulis matriks A =  , dengan
, dengan  adalah elemen matriks A dengan i = 1,2,...,m dan j = 1,2,...,n.
adalah elemen matriks A dengan i = 1,2,...,m dan j = 1,2,...,n.
Atau matriks A dapat ditulis dalam bentuk:
Contoh:
dengan i = 1,2,3,4 dan j = 1,2,3,4. Tentukan matriks A
Jawab
Submatriks dari matriks A adalah sembarang matriks yang didapatkan dengan cara menghilangkan beberapa baris atau kolom tertentu dari matriks A. Matriks A sendiri dapat dipandang sebagai submatriks dari A.
Contoh:
Bentuk Matriks Khusus
- Suatu matriks disebut matriks segi, jika banyaknya baris sama dengan banyaknya kolom. Jika banyaknya kolom = banyaknya baris = n, maka matriks tersebut dikatakan matriks segi berordo n atau berukuran n. Sedangkan elemen elemen
disebut elemen diagonal utama.
- Suatu matrik segi disebut matriks segitiga atas, jika elemen di bawah diagonal utama bernilai nol. Sedangkan matriks segitiga bawah, jika elemen di atas diagonal utama bernilai nol.
- Suatu matriks segi disebut matriks identitas, jika semua elemen diagonal utamanya bernilai satu, sedangkan yang lainnya bernilai nol. Matriks identitas berukuran n, diberi notasi
.
Contoh:
OPERASI MATRIKS
Penjumlahan, Pengurangan, dan Perkalian Matriks serta Perkalian dengan Skalar
Tinjau A dan B dua matriks yang berukuran sama, misalkan ukurannya m x n
Penjumlahan dan pengurangan matrik A dan B, ditulis A B adalah matriks yang diperoleh dengan menjumlahkn elemen-elemen yang seletak antara matriks A dan B, yaitu:
B adalah matriks yang diperoleh dengan menjumlahkn elemen-elemen yang seletak antara matriks A dan B, yaitu:
Penjumlahan dan pengurangan matrik tidak dapat dilakukan jika kedua matriks berbeda ukurannya.
Perkalian skalar k dengan matriks A, ditulis kA, adalah matriks yang diperoleh dengan mengalihkan setiap elemen A dengan skalar k, yaitu:
Contoh:
Misalkan matriks
Hukum-Hukum pada Penjumlahan/Pengurangan dan Perkalian Skalar
Catatan: O adalah matriks nol, yaitu matriks yang semua elemennya nol.
Perkalian Matriks
Tinjau matriks A = (), dan B = (), dengan banyaknya kolom matrik A sama dengan banyaknya baris matriks B. Misalkan A berukuran m x p dan B berukuran p x n, maka matriks hasil kali A dan B adalah berukuran m x n yang elemen ke-ij diperoleh dari mengalikan baris ke-i dari matriks A dengan kolom ke-j dari matriks B, seperti dibawah ini.
dengan,
Contoh
Misalkan matriks
Perhatikan, ukuran matriks A adalah 2 x 3 dan matriks B berukuran 3 x 1, sehingga matriks hasil perkalian AB berukuran 2 x 1 seperti berikut:
Hukum-Hukum pada Perkalian Matriks
- ( A B ) C = A ( B C ) Hukum assosiatif
- A ( B + C ) = A B + A C Hukum Distributif Kiri
- ( B + C ) A = B A + C A Hukum Distributif Kanan
- k ( AB ) = ( k A ) B = A ( k B) k skalar
Catatan: AB # BA
Contoh:
Misalkan matriks
maka:
dari contoh di atas dapat dilihat bahwa, 3A +3B = 3(A+B)






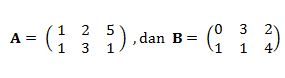
0 Response to "Penjumlahan dan Pengurangan Dan Perkalian Matriks Dengan Skalar"
Post a Comment